Welcome to our in-depth guide on Class 9 Science Chapter 9: Force and Laws of Motion! If you’re a Class 9 student preparing for your 2025 CBSE exams, a parent assisting your child with Physics, or a teacher seeking comprehensive resources, this blog post is your ultimate resource. We’ll cover the in-text questions and answers, exercise solutions, and detailed notes for Chapter 9, breaking down the concepts of force, inertia, and Newton’s laws into clear, thorough explanations. By the end, you’ll have a deep understanding of how forces govern motion—equipping you to excel in your exams and strengthen your Physics foundation!
Chapter 9 explores the relationship between force and motion, introducing Newton’s groundbreaking laws that explain everyday phenomena like a ball rolling or a car stopping. Let’s dive into the Class 9 Science Chapter 9 questions, answers, and notes!
Class 9 Science Chapter 9 Notes
1. Force
- Definition: A push or pull that can change an object’s state of rest, motion, or shape.
- Types:
- Balanced Forces: Equal, opposite forces; no change in motion (e.g., a book on a table).
- Unbalanced Forces: Cause motion or acceleration (e.g., kicking a ball).
- Unit: Newton (N), where 1 N = 1 kg·m/s².
2. Inertia
- Definition: Tendency of an object to resist changes in its state of motion.
- Dependence: Proportional to mass—greater mass, greater inertia.
- Examples: A heavy rock resists moving; a light feather stops easily.
3. Newton’s Laws of Motion
- First Law (Law of Inertia): An object remains at rest or in uniform motion unless acted upon by an unbalanced force.
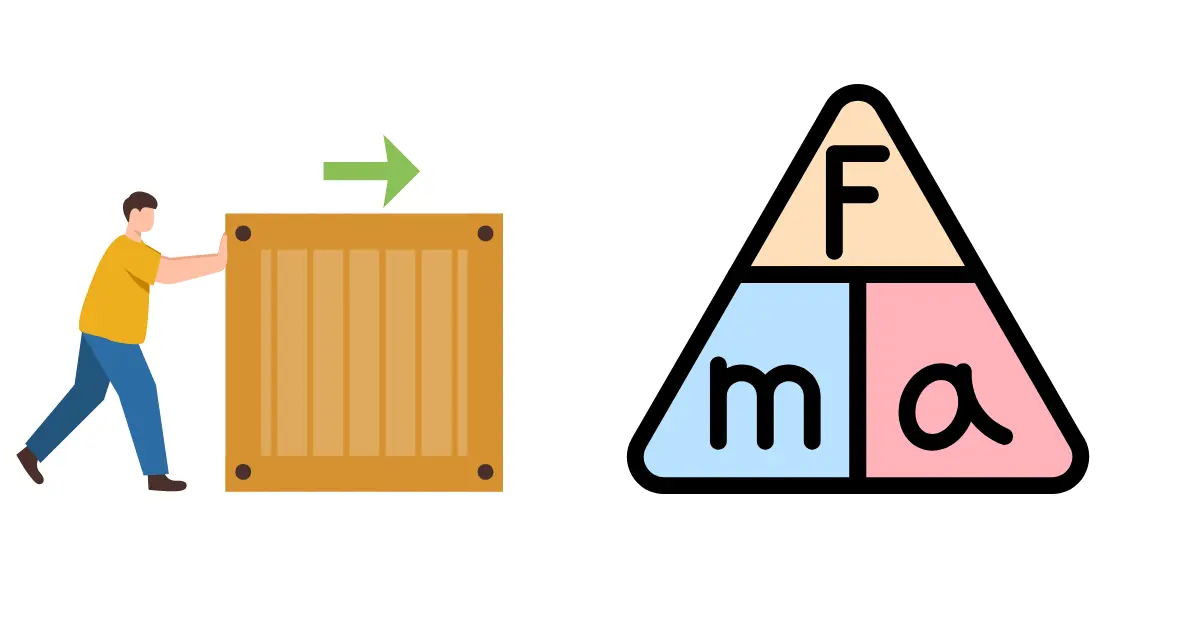
- Second Law: Force = Mass × Acceleration (F = ma); force determines how much an object accelerates.
- Third Law: For every action, there’s an equal and opposite reaction (e.g., rocket propulsion).
4. Momentum
- Definition: Product of mass and velocity (p = mv), a vector quantity.
- Unit: kg·m/s.
- Conservation: Total momentum before and after a collision remains constant if no external force acts.
5. Applications
- First Law: Seat belts prevent passengers from moving forward during a sudden stop.
- Second Law: Pushing a cart harder increases its acceleration.
- Third Law: Walking involves pushing the ground backward, which pushes you forward.
These notes summarize the chapter’s core ideas—use them as a foundation for the Q&As!
In-Text Questions and Answers: Page 118
Question 1: Provide an exhaustive explanation of which property of an object determines how much inertia it possesses, and elaborate on how this property influences the object’s behavior when subjected to external forces in various real-life scenarios.
Answer:
The property of an object that determines how much inertia it possesses is its mass. Inertia, often described as the resistance of an object to changes in its state of motion—whether it’s at rest or moving—directly depends on how much matter an object contains. The greater the mass, the more inertia an object has, meaning it requires more force to start, stop, or alter its motion. This stems from Newton’s First Law, which states that an object will maintain its current state unless acted upon by an unbalanced force. Let’s explore this in real-life scenarios.
Consider a heavy truck versus a bicycle: pushing the truck from rest takes immense effort because its large mass gives it high inertia, resisting the change to motion. The bicycle, with less mass, moves easily with a gentle push. Similarly, stopping a rolling bowling ball (high mass, high inertia) requires more force—say, a strong kick—than stopping a ping-pong ball (low mass, low inertia), which a light tap can halt. In another example, a massive ship at sea keeps moving forward even after its engines stop due to its enormous inertia, while a small boat slows quickly.
Mass influences behavior by dictating how much force is needed to overcome inertia, affecting everything from sports (e.g., a heavier shot put resists throwing) to safety (e.g., seat belts counter a body’s inertia in a crash). Thus, mass is the key determinant, shaping how objects respond to external forces in diverse situations.
Question 2: Discuss in detail why some objects are inherently more difficult to move than others, including the underlying physical principles and examples that illustrate this phenomenon across different contexts.
Answer:
Some objects are inherently more difficult to move than others primarily due to their mass, which governs their inertia—the resistance to changes in motion—as outlined by Newton’s First Law. The underlying principle is that inertia increases with mass: a heavier object has more matter, making it harder to start moving from rest or stop once in motion, because a greater force is required to overcome its tendency to maintain its current state. Friction also plays a role, but inertia is the core reason tied to mass.
Let’s illustrate this with detailed examples across contexts. A massive boulder on a hillside is tough to budge—its high mass means even a strong push might not suffice, as its inertia resists the change from rest. Compare this to a pebble, which a light nudge can roll easily due to its low mass and minimal inertia. In sports, a cricket ball (about 160 g) is easier to throw than a shot put (7.26 kg for men), where athletes strain against its greater inertia. In transportation, a fully loaded truck takes longer to accelerate from a stoplight than a small car, as the truck’s larger mass demands more engine force to overcome inertia.
Even in space, a massive satellite requires powerful rockets to shift its orbit, while a tiny probe adjusts with less thrust. These examples show that difficulty in moving objects stems from mass-driven inertia, a principle affecting daily tasks, engineering, and natural phenomena, highlighting why heavier objects consistently demand more effort to set into motion or alter their path.
In-Text Questions and Answers: Page 126
Question 1: Explain comprehensively why a moving object eventually comes to a stop when no external force is applied to maintain its motion, incorporating the role of opposing forces and real-world instances where this occurs.
Answer:
A moving object eventually comes to a stop when no external force is applied to maintain its motion due to the presence of opposing forces, most commonly friction, which counteract its momentum and reduce its velocity over time. According to Newton’s First Law, an object in motion should continue moving indefinitely in a straight line at constant speed unless acted upon by an unbalanced force. However, in real-world conditions, forces like friction (between surfaces), air resistance, or water drag act as external influences that oppose motion, gradually bringing the object to rest.
Friction arises when two surfaces rub against each other, converting kinetic energy into heat, while air resistance pushes against objects moving through the atmosphere. Let’s explore this with examples.
A ball rolling on grass slows and stops because friction between the ball and the uneven ground opposes its motion, absorbing its energy—on a smoother ice rink, it rolls farther due to less friction. A car coasting after the engine is turned off eventually halts as friction from the road and air resistance work against its forward momentum; brakes amplify this effect.
A boat drifting on water stops as water drag resists its glide. Even a hockey puck on ice, though low-friction, eventually rests due to slight air resistance and ice imperfections. These opposing forces ensure that, without a continuous push (like an engine or kick), motion dissipates, aligning with the practical reality that perpetual motion is impossible on Earth due to these ever-present counterforces.
Question 2: Provide an extensive analysis of why a fielder in a cricket match gradually lowers their hands while catching a fast-moving ball, connecting this action to the principles of physics and its practical implications.
Answer:
A fielder in a cricket match gradually lowers their hands while catching a fast-moving ball to reduce the force exerted on their hands, a technique rooted in Newton’s Second Law (F = ma) and the concept of impulse, which is the change in momentum (Force × Time). When a ball travels at high speed, it carries significant momentum (p = mv), and stopping it abruptly requires a large force over a short time, potentially hurting the fielder’s hands. By lowering their hands gradually, the fielder increases the time over which the ball’s velocity decreases from its initial value to zero, thus reducing the acceleration (a = Δv/Δt).
Since force is mass times acceleration (F = ma), a smaller acceleration (due to longer time) means a smaller force on the hands. For example, if a 160 g ball moving at 20 m/s stops in 0.1 s, the force is F = (0.16 × 20) / 0.1 = 32 N. If the fielder extends the stopping time to 0.5 s by lowering their hands, the force drops to (0.16 × 20) / 0.5 = 6.4 N—far less painful! This action mirrors real-world physics: a car’s airbag works similarly, cushioning impact by extending collision time.
Practically, this technique prevents injury, improves catch success (less chance of dropping due to pain), and showcases how physics enhances sports strategy. The fielder intuitively applies impulse principles, spreading the momentum change over time, making the catch safer and more effective.
Exercise Questions and Answers: Page 134
Question 1: An object experiences a net zero external unbalanced force. Discuss in detail whether this object will be at rest or in motion, and explain the conditions under which each scenario could occur, with examples.
Answer:
When an object experiences a net zero external unbalanced force, it could either be at rest or in uniform motion, depending on its initial state, as dictated by Newton’s First Law. This law states that an object remains in its current state—rest or motion—unless an unbalanced force acts on it. A net zero force means all forces acting on the object (e.g., push, pull, friction) balance out, leaving no resultant force to change its motion. If the object is initially at rest, it stays at rest because no unbalanced force accelerates it.
For instance, a book on a table remains stationary: gravity pulls it down, the table pushes up equally, and no horizontal force moves it—net force is zero.
If the object is initially moving, it continues in uniform motion (constant speed, straight line). Consider a hockey puck sliding on frictionless ice: once pushed, it glides indefinitely because no opposing force (friction is negligible) alters its motion—net force remains zero. In space, a satellite moves steadily with zero net force (gravity balanced by orbital motion). The key condition is the absence of unbalanced forces: at rest if stationary to start, or moving if already in motion. Real-world friction often complicates this, but in ideal scenarios (e.g., vacuum), these states persist, illustrating inertia’s role in maintaining an object’s behavior when forces cancel out.
Question 2: A truck of mass 1200 kg moving with a velocity of 90 km/h collides with a stationary car of mass 800 kg. After the collision, they move together. Calculate in detail the common velocity after the collision, including all steps, unit conversions, and the physical principle involved.
Answer:
To calculate the common velocity after the truck (1200 kg, 90 km/h) collides with the stationary car (800 kg) and they move together, we use the law of conservation of momentum, which states that total momentum before and after a collision remains constant if no external forces (like friction) act significantly. Momentum is mass × velocity (p = mv). Let’s solve this step-by-step.
- Convert units: Initial velocity of truck = 90 km/h. Convert to m/s: 90 × (1000/3600) = 90 × 5/18 = 25 m/s. Car’s initial velocity = 0 m/s (stationary).
- Before collision:
- Truck momentum = 1200 × 25 = 30,000 kg·m/s.
- Car momentum = 800 × 0 = 0 kg·m/s.
- Total momentum = 30,000 + 0 = 30,000 kg·m/s.
- After collision: They move together with a common velocity (v). Total mass = 1200 + 800 = 2000 kg.
- Total momentum = (2000) × v.
- Conservation equation: Momentum before = Momentum after.
- 30,000 = 2000 × v.
- v = 30,000 / 2000 = 15 m/s.
- Verification: Convert back: 15 m/s × (18/5) = 54 km/h.
The common velocity is 15 m/s (or 54 km/h). This inelastic collision (they stick together) conserves momentum, not kinetic energy, as some energy dissipates as heat/sound. The truck’s higher mass and speed dominate, but the combined mass reduces the final velocity, showing how momentum redistributes in real crashes, like vehicles merging in accidents.
Class 9 Science Chapter 9: Force and Laws of Motion reveals the mechanics behind movement and rest, from inertia to action-reaction pairs, preparing you for your 2025 CBSE exams. With these detailed notes, extended questions, and solutions, you’re equipped to tackle any force-related problem. This chapter blends theory with practical applications, making it both intriguing and vital.
For more practice, check NCERT solutions and sample papers online. Have doubts? Drop them in the comments—we’re here to help! Keep studying and stay curious!
For all Class 9 Science Chapters: Notes and Question Answers. Click Here.
1 thought on “Class 9 Science Chapter 9: Force and Laws of Motion – Questions, Answers, Exercise Solutions, and Notes”